About
Educational tools for quantum information science
Want to know more?
If you want to know more or for whatever reason want to contact us, please Do not hesitate to do so.
Toolkits
There are four standard toolkits available
Customized Orders
We can also produce toolkits for Grover's and the Bernstein-Vazirani algorithm. If you have something else in mind, please contact us with a request.
Submit a RequestQuantum Key Distribution
The key is generated by Alice sending qubits to Bob, encoding bit values into a randomly chosen encodings. Bob measures the qubits in other randomly chosen encodings. They compare the encodings and save only the bits where they chose the same. If someone eavesdrops on the quantum channel, this will be visible as bit errors in the generated key.


Teleportation & Superdense coding
Quantum teleportation enables Bob to recreate an unknown quantum state in the posession of Alice. This is possible if they share an entangled pair of systems, and needs only two classical bits of information to be transmitted from Alice to Bob. Superdense coding, on the other hand, enables Alice to send Bob a message of two classical bits by only interacting with one qubit of an entangled pair.
The Deutsch-Jozsa Algorithm
The Deutsch-Jozsa problem is to determine whether a Boolean function is constant or balanced. A constant function returns the same output for all possible input values, while a balanced function returns zero for half of them and one for the others.
In classical query complexity a number of function calls exponential in the input size is needed, while the quantum algorithm can solve the problem with only one call.

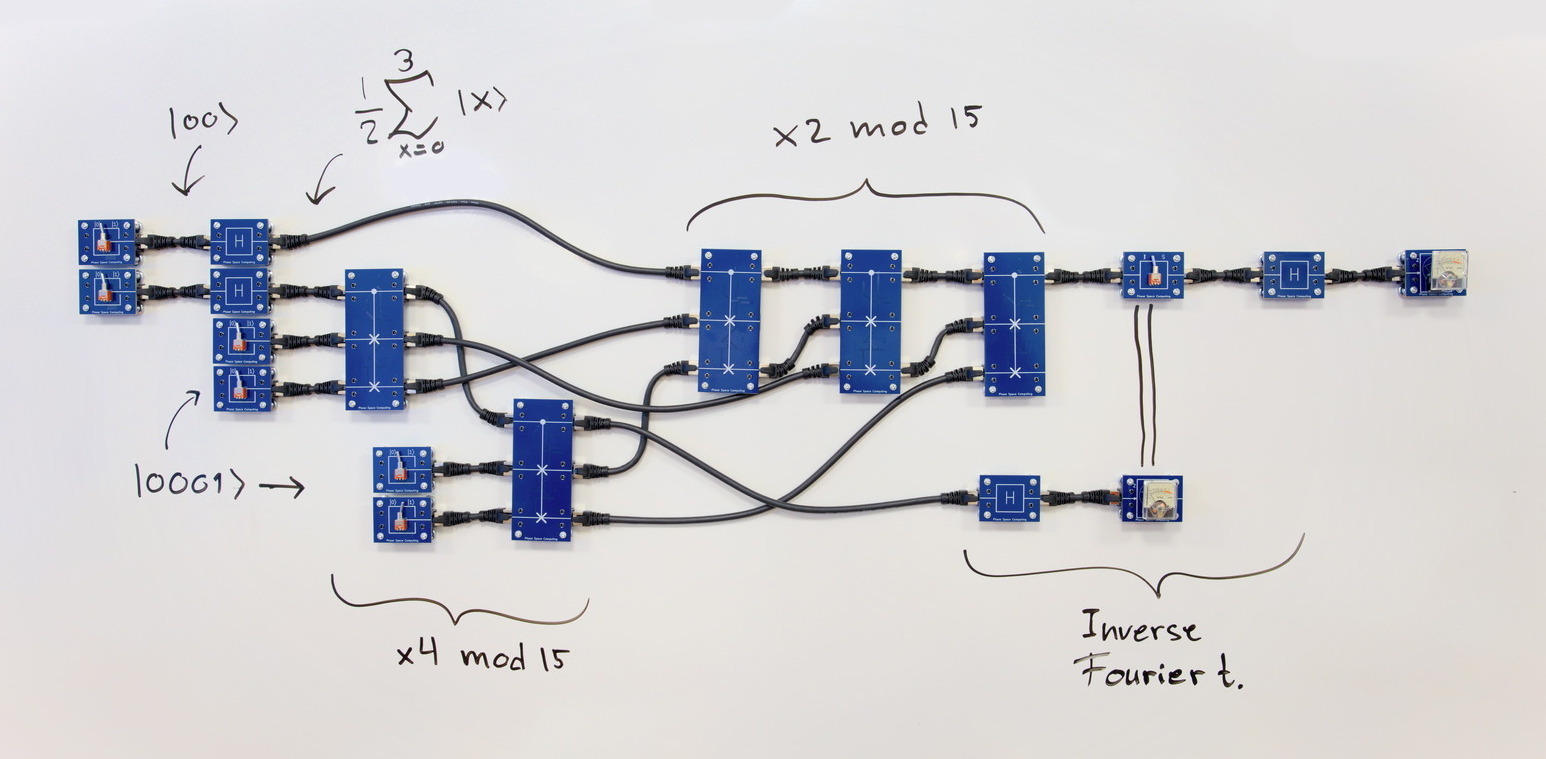
Shor's Algorithm
Shor's quantum algorithm can be used to factor large integers efficiently in a quantum computer. This is currently believed to be a hard problem for ordinary computers. Building a quantum computer is currently difficult and a research subject at many universities and companies. This toolbox provides an interactive experience where students gradually work their way to an understanding of Shor's algorithm.
Gates
The building blocks

X

H

Source
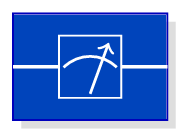
Meter
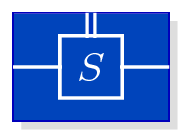
S

X
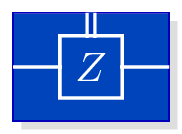
Z

H
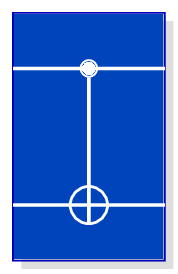
CNOT

Toffoli

Fredkin






















Technology
How does it work?
Kit Contents
What you get

Quantum Key Distribution
- 2X Source
- 2X Measurement
- 4X Classically controlled H
- 1X CNOT
- Example curricula
- Patch cables
- Power supply
Teleportation & Superdense coding
- 3X Source
- 3X Measurement
- 2X Hadamard
- 2X Classically controlled H
- 2X Classically controlled S
- 1X Classically controlled X
- 1X Classically controlled Z
- 2X CNOT
- Example curricula
- Patch cables
- Power supply
The Deutsch-Jozsa Algorithm
- 4X Source
- 3X Measurement
- 7X Hadamard
- 1X Pauli-X
- 3X CNOT
- 2X Toffoli
- Example curricula
- Patch cables
- Power supply
Shor's Algorithm
- 6X Source
- 4X Measurement
- 1X Classically controlled S
- 4X Hadamard
- 4X CNOT
- 5X Fredkin
- Example curricula
- Patch cables
- Power supply
Contact
Phase Space Computing AB
Address
-
Rydsvägen 280
58439
Linköping, Sweden - sales@phasespacecomputing.com
- info@phasespacecomputing.com
